Monetary economists have long advocated rules-based monetary policy to improve macroeconomic outcomes by limiting central bankers’ discretion. A problem with implementing this approach is that public officials do not want a strict rule that prevents them from changing their policy stance, especially when unforeseen circumstances arise. The 2015 Fed Oversight Reform and Modernization Act (FORM Act) was drafted to mitigate this problem. Had it passed, the bill would have required the Federal Reserve (Fed) to set a policy rule, only allowing the Fed to suspend the rule if it publicly explained its reasoning to Congress.¹

Policy rules have been popular in the academic literature for decades. For instance, Milton Friedman famously argued in the 1960s for the Fed to adopt a zero nominal interest rate environment (often dubbed the Friedman rule).² Rules-based monetary policy gained further popularity and academic significance when, in 1993, John Taylor found that a simple rule that adjusted the policy rate as a weighted response to inflation and the output gap (the difference between gross domestic product [GDP] and potential GDP) was able to closely match the realized federal funds rate.³ In the modern New Keynesian macroeconomic framework, interest rates are often modeled as a generalized feedback rule, similar in spirit to the 1993 Taylor rule but with different weights or modified components (replacing or adding to inflation and the output gap, for instance).

The potential benefits of such rules-based monetary policy are numerous and are discussed in further detail in the section “Benefits of Rules-Based Monetary Policy.” However, simply advocating for the Fed to follow a rule is insufficient because a bad policy rule could lead to adverse economic outcomes. Complicating matters, economists disagree over which specific feedback rule is best. Several academic models calibrate the feedback rule to match the 1993 Taylor rule. Some argue for using output growth instead of the output gap. Yet others argue for a rule that is calibrated to target nominal spending.⁴ Luckily, many of these rules are mathematically similar, and they are all designed to respond to short-term shocks that move the economy away from its long-term equilibrium path.⁵

Ultimately, which rule the Fed should follow depends on two key factors: the informational burden the rule will impose on the central bank and the degree to which it might stabilize macroeconomic variables. The section “Comparison of Feedback Rule Information Burdens” compares the informational burdens faced by the Fed when forecasting various macroeconomic variables with the corresponding effects of forecast errors when the Fed incorporates these variables across various feedback rules. The section “Structural Macroeconomic Analysis” uses the 2007 dynamic stochastic general equilibrium, or DSGE, model created by Frank Smets and Rafael Wouters to simulate the US economy across various feedback rules to determine which iteration might best stabilize the economy.

No rule is the clear winner. Output gap rules perform well at stabilization but suffer from nonstationarity in the Fed’s forecasts.⁶ However, rules that offer informational advantages, such as those that target only inflation or a combination of output growth and inflation, are unlikely to produce near-optimal macro stabilization. The data show that rules perform better or worse at producing stabilization depending on their responses to demand or supply shocks.

The key takeaway is that debates among experts over the superiority of various rules should not hamper the Fed’s immediate commitment to following a rule. Virtually any rule under consideration is imperfect and has different costs and benefits: informational burdens versus macroeconomic stability, better responses to demand versus supply, and so on. Moreover, central banks are ill-suited to “manage” the economy by consistently reaching precise macroeconomic goals. Since no one rule is plainly best and most rules under consideration are better than discretion, the Fed should decide which of the various trade-offs are most desirable and credibly commit to following the rule associated with them. To ensure that the Fed and elected officials remain accountable for monetary policy decisions, Congress should require the Fed to adopt rules-based monetary policy.

Rules-based monetary policy gives central banks a set of guidelines that dictate their current and future actions. Proponents of such rules date back as far as 1936, when Henry Simons wrote that such a rule “avoids reliance on discretionary (dictatorial, arbitrary) action by an independent monetary authority and defines a statutory rule which might be enacted by the competent legislature.”⁷ Presently, the Fed employs discretionary monetary policy without any explicit rule. The Fed does operate under the so-called dual mandate—statutory language that directs it to promote both price stability and maximum sustainable employment—but it has no binding requirements to achieve any specific economic goals regarding price, unemployment, or other macro variables.⁸

Under this discretionary framework, the Fed is free to judge both the direction of the economy and the appropriate monetary policy response. In general, if the Fed believes there is a danger of deflation (a falling price level) or of unemployment rising quickly, it pursues expansionary policy. If, however, the Fed believes that unemployment is unsustainably low or that there is a danger of inflation, it follows a contractionary policy. Yet the Fed is not bound to implement expansionary or contractionary policies at any time using any benchmark.

Advocates of discretion-based policy claim that the enormous complexity of the ever-changing economy requires such broad discretion. But the opposite is true. No one person—or small group of central bankers—can ever be expected to understand and react properly, much less to always act consistently, to changing conditions throughout the economy. The Fed does not possess the technocratic prowess to reach precise macroeconomic goals.⁹ Meticulous management should not be the goal of monetary policy.

Instead, the goal of monetary policy should be to reduce uncertainty by anchoring people’s expectations concerning what the Fed will do on an ongoing basis. Providing clarity with respect to the Fed’s policy decisions is also critical to holding both appointed and elected officials accountable for their decisions. Rules-based monetary policy can improve accountability and anchor expectations by overcoming a major credibility problem that the Fed faces: The Fed cannot—under a discretionary framework—credibly commit to any future course of action. This is because of the “time inconsistency” problem.¹⁰ It occurs because decisions that seem optimal at one time become less suitable due to changes in the economic environment later. Economic agents know this and are unlikely to trust the Fed’s commitment to following through on its promised course of action. An explicit policy rule would alleviate some of these credibility concerns.

A clear policy rule represents a commitment. In the case of monetary policy, this rule would bind the Fed to a future course of action based on clearly defined economic outcomes. Naturally, such a commitment would reduce uncertainty surrounding future monetary policy changes. If properly structured, a monetary policy rule would also help prevent short-term considerations—such as temporary cyclical fluctuations—from interfering with the Fed’s long-term goals. Even a rule that specifies a range of policy options can help insulate a central bank from short-term factors that hinder its long-term goals, including undue political influence.¹¹

The empirical literature shows that rules also improve economic outcomes. For instance, Alex Nikolsko-Rzhevskyy and others found that the Fed implicitly followed a rule from 1966 to 1974 and again from 1985 to 2000, but not in between and not after.¹² Their paper shows that economic performance was better under a rules-based framework, but the degree of benefit depended on the type of rule. John Taylor also found a rules-based period from 1985 to 2003 followed by an ad hoc discretionary period after 2003. Taylor concludes that economic performance was worse in the discretionary period.¹³ Finally, Jai Kedia analyzed Fed policy by extending this sample through 2022 and concludes that discretionary behavior has become more prevalent since 2009, with each successive Fed administration being more discretionary than its predecessor.¹⁴

Central banks face knowledge problems arising from the difficulty of collecting and forecasting the variables to which they must respond. Given this inherent difficulty, the Fed always risks setting an interest rate target that is off course due to inaccurate measures, either real-time or forecasted, of variables such as prices and output. Such inaccuracy in data observations, and therefore in policy rate decisions, can lead to inefficacy at best and counterproductive policy at worst.

For instance, Athanasios Orphanides argues that, contrary to conventional thinking about the failings of monetary policy, policymakers in the 1970s chose policies similar to those of their modern counterparts, given the information available to them, despite the failure of monetary policy to prevent stagflation.¹⁵ This is because the real-time estimates of the nonaccelerating inflation rate of unemployment—the “potential” level of “full” employment in the economy—were poor and policymakers who relied on these estimates were basing policy rate decisions on bad data. Like potential employment, it is also difficult for policymakers to accurately measure the economy’s potential output. This data challenge is problematic since most interest rate feedback rules require the Fed to respond to changes in overall output, often represented by the US output gap.

Several academics have singled out the output gap as the biggest source of informational constraints a central bank faces. For instance, David Beckworth and Joshua R. Hendrickson used an augmented Dickey–Fuller test to show that the Fed’s errors in forecasting the output gap may be nonstationary, as the test fails to reject the null hypothesis of a unit root.¹⁶ While not a standard measure of forecast accuracy, nonstationary time series may indicate an unstable underlying model. The Beckworth and Hendrickson analysis contrasts the output gap with nominal GDP, showing the latter to be stationary and, therefore, better suited as a response variable for the central bank. However, as the analysis presented in this section shows, the same is true for most other macro indicators typically included in a feedback rule. In other words, many other macroeconomic time series that could be included in the Fed’s feedback rule are also stationary.

To analyze the information burdens of various feedback rules, we used Fed forecast data available in the Fed’s Tealbook (formerly Greenbook) datasets, which are produced before every meeting of the Federal Open Market Committee to help guide policy decisions.¹⁷ Using these data, we aggregated forecasts by averaging them to a quarterly frequency from 1996 through 2018. We then compared all forecasts with their realized counterparts to compute forecast errors. (All realized data were collected from the Federal Reserve Economic Database, maintained by the St. Louis Fed.) For all analyses, findings are presented for Fed forecast errors ranging from the same quarter at time t (i.e., a “nowcast”) through t + 4 quarters ahead.

Table 1 shows the critical statistics from an augmented Dickey–Fuller test conducted on the Fed’s forecast errors for various macro indicators that may be included in a standard policy rate feedback rule. These indicators include the output gap (ogap_t), real GDP growth (%Δrgdp_t), nominal GDP growth (%Δngdp_t), inflation (π) measured by the GDP deflator (PGDP), and inflation (π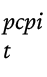) measured by the Consumer Price Index (PCPI).

For the Dickey–Fuller test, the null hypothesis cannot be rejected only in the case of the output gap. That is, other than the output gap, all the macro time series commonly included in a feedback rule are stationary, as is nominal GDP. If stationarity is indeed the correct measure for selection, then it is not immediately clear that nominal GDP is the only rule that satisfies this condition. The Fed could, for instance, use a disaggregated feedback rule (i.e., it could target output and prices separately) with various inflation or output metrics (except the output gap) and still maintain stationarity.¹⁸ In fact, insofar as the magnitude of the Dickey–Fuller test statistics are relevant, inflation as measured by the PCPI offers a firmer rejection of the null hypothesis than even nominal GDP.

Of course, the Dickey–Fuller test is generally not used to measure forecast accuracy, another important criterion. Instead, forecast accuracy is traditionally evaluated using the magnitude of the forecast errors themselves. However, to prevent errors that cancel each other out from causing the Fed to overshoot or undershoot a forecast, individual forecast errors are typically squared and then summed across the entire period. Table 2 displays this “sum of squared error” metric for all variables and corresponding lags used in the Dickey–Fuller tests in Table 1.¹⁹

The forecast error comparison shows that nominal GDP has the lowest degree of forecast accuracy. Inflation computed using the GDP price index (also conveyed as PGDP) has the highest degree of forecast accuracy across most horizons. Interestingly, the Fed has very few errors in nowcasting CPI inflation, but this error increases drastically when forecasting CPI inflation. In other words, the Fed’s estimates of real-time CPI inflation are good, but its forecasts of future CPI inflation are poor.

Of course, a proponent of nominal GDP targeting may argue that it is unfair to compare aggregate measures of the economy, such as nominal GDP, to measures that track prices or output individually. Since nominal GDP includes both prices and output, a researcher would expect it to have a higher degree of uncertainty than price/​output measures alone. On the surface, this expectation appears to hold up—the sum of forecast errors for real GDP and PGDP exceeds nominal GDP at every horizon other than nowcasts. However, this evaluation is incomplete because feedback rules are often weighted averages of various macro indicators.

Under traditional parameterizations of a feedback rule, the central bank places a higher weight on inflation than output. For instance, the original 1993 Taylor rule would imply that the Fed targets inflation with a weight of 1.5 compared with a weight of 0.5 on the output gap. Using this kind of rule, with PGDP as the price measure, the Fed would rely more heavily on a more forecastable variable and less on the more difficult-to-forecast output measures. Conversely, a feedback rule calibrated for nominal GDP targeting would place all its weight on a poorly forecasted variable: aggregate nominal GDP changes. That weight could be 1 or higher—such as 1.78, the weight chosen by Beckworth and Hendrickson in their 2019 paper.²⁰

In the end, the feedback rule calibration that results in the smallest forecast error depends on these choices of weights and is empirically testable. Table 3 provides the results from such a test, presenting the sum of squared forecast errors from several formulations of a feedback rule. The tests are run on every combination of price (inflation as measured by the PCPI and PGDP) and output (output gap and real GDP) metrics with the standard 1993 Taylor rule parameters and two weight calibrations for nominal GDP targeting: 1 and 1.78. A key benefit of analyzing forecast errors this way is that the disaggregation of the rule into prices and output allows forecast errors across these variables to offset one another. That is, if the Fed tends to overshoot inflation but undershoot output in the same period, or vice versa, it leads to lower net forecast errors for the final policy rate. However, if the Fed’s forecast errors of these variables tend to occur in the same direction, it can have drastic aggregated effects on the prescribed policy rate.

Table 3 shows several important findings. First, nowcasts aside, feedback rules using CPI inflation fare significantly worse than those using PGDP inflation. Second, simple nominal GDP targeting (i.e., with a response parameter of 1) outperforms feedback rules with CPI inflation, but nominal GDP targeting with a coefficient of 1.78 performs similarly to the Taylor rules using CPI inflation. Still, the lowest forecast errors are associated with a feedback rule using PGDP inflation and real GDP growth.

While it is unsurprising that PGDP inflation, the most accurately forecasted variable, is included in the rule with the least informational burdens, the data are consistent with the arguments of many nominal GDP targeting proponents, as they show a benefit in using output growth rather than the output gap. This finding holds despite output gap forecast errors being lower than real GDP growth forecast errors. This finding also suggests that Fed forecast errors in PGDP inflation and GDP growth usually offset, leading to smaller negative informational effects on the final policy rate. While this smaller effect may be surprising on the surface, recall from Table 1 that output gap measures may exhibit a unit root. As such, when the Fed is wrong about the output gap, it tends to continue to be wrong in the same direction. Consequently, it is difficult for the Fed to realize any gains from forecast error offsets when using the output gap.

These findings should be good news for policymakers. They suggest that the Fed can alleviate some of its information burdens without radically departing from its adherence to the types of rules it followed during the Great Moderation, a period of low inflation and economic stability in the United States from the 1980s to the 2007 financial crisis. At the very least, these analyses show that the debate over which of these feedback rule formulations best lowers the Fed’s information burden is useful. They also should not stop proponents of nominal GDP targeting from agreeing that Congress should mandate the Fed to use a rule, even if that rule follows formulations similar to the traditional Taylor rule, with disaggregated and uneven responses to inflation and output.

This section analyzes the welfare effects of various feedback rules using a large structural macroeconomic model. We broadly followed the method used by the 2019 Beckworth and Hendrickson paper (henceforth BH2019), but our analysis offers a few advantages over the prior literature. First, we used the 2007 Smets and Wouters (henceforth SW2007) framework as the base model.²¹ This model is considered a benchmark for empirical macroanalysis and includes several desirable features missing from simpler models. These features—such as habit formation, variable capital utilization, investment adjustment costs, price and wage stickiness, and others—significantly improve the model’s ability to fit the US economy. As such, welfare analyses conducted using this framework are more reliable and less prone to bias from omitted variables. Another advantage is that SW2007 also forms the core of the New York Fed’s in-house DSGE model.²²

Second, our welfare analysis encompasses the volatility of the policy rate itself. Traditionally, such welfare analyses have been limited to checking the volatility of inflation and output in response to variations in the model’s parameters or equation structures. However, excluding the interest rate from the analysis is unrealistic because policymakers are typically unwilling to make large changes to their policy instrument, even if it means immediate reductions in inflation or output volatility. This phenomenon has been evident from the Fed’s actions going back to the 1970s or even earlier.²³ Owing to this phenomenon, some academic treatments of welfare often add interest rate deviations along with inflation and output fluctuations to a loss function that is to be minimized by a welfare-optimizing central bank.²⁴

Recent empirical evidence also suggests that interest rate changes directly affect consumer utility. As recently as 2023, with inflation trending back toward target after its post-pandemic high and unemployment remaining below 4 percent, consumer sentiment remained depressed and still below its pre-pandemic levels. Marijn Bolhuis and others have demonstrated that concerns over borrowing costs could help explain this sentiment puzzle, suggesting that interest rates play a key role in consumer utility.²⁵ Thus, including interest rates in a welfare analysis is more realistic from the perspective of a sensible policymaker and from a consumer welfare perspective.

The full derivation of the SW2007 model is beyond the scope of this paper, so we present only a summary of the equilibrium equations for the model.²⁶ The model structurally relates the following 14 macro variables presented as log deviations from their respective steady states: output (y_t), consumption (c_t), investment (i_t), capital utilization (z_t), labor hours supplied (l_t), interest rate (r_t), inflation (π_t), value of capital stock (q_t), rental rate of capital (r), capital services (k), aggregate capital stock (k_t), price markup (μ), wages (w_t), and the wage markup (μ). Additionally, the economy is subject to seven per-period random disturbances that cause it to fluctuate from its steady state: exogenous spending (ε), risk premium (ε), investment-specific technology (ε), productivity (ε), price markup (ε), wage markup (ε), and monetary policy (ε). Symbols that do not bear time subscripts represent constant positive parameters. The equilibrium equations of the model are as follows:

Aggregate resource constraint:

(1)

Consumption Euler equation:

(2)

Investment Euler equation:

(3)

Arbitrage equation for value of capital:

(4)

Aggregate production function:

(5)

Evolution of capital services:

(6)

Degree of capital utilization:

(7)

Capital accumulation:

(8)

Goods market price markup:

(9)

New Keynesian Phillips curve:

(10)

Rental rate of capital:

(11)

Labor market wage markup:

(12)

Wage relation:

(13)

Monetary policy feedback rule:²⁷

(14)

The evolution of the disturbances is also taken directly from SW2007, where all disturbances have corresponding per-period IID shocks (η_t).²⁸ The processes for the seven model disturbances are presented below:

Risk premium:

(15)

Exogenous spending:

(16)

Investment-specific technology:

(17)

Productivity:

(18)

Price markup:²⁹

(19)

Wage markup:

(20)

Monetary policy:

(21)

The welfare analysis used to evaluate optimal monetary policy rules relies on numerous simulations under various policy rules. None of the policy rules under consideration require a drastic change to the framework described in the section “Model Summary.” Instead, all the various policy rules simply require parameter or variable adjustments to the monetary policy feedback rule shown in equation 14. Aside from the parameters and structure of the monetary policy feedback rule, the model is maintained exactly as described in the “Model Summary” section. For all analyses, we have fixed the model parameters at their posterior means as reported in Table 1a of SW2007. Equation 14 is then varied to analyze welfare under different monetary policy rate rules. The various policy rate rules under consideration are as follows:

1. Standard Taylor rule (where ρ = 0.8, r_π = 1.5, and r_y = 0.5):

(22)

2. Smets and Wouters (2007) (where ρ = 0.81, r_π = 2.04, r_y = 0.08, and r_Δy = 0.22):

(23)

3. Beckworth and Hendrickson (2019) (where ρ = 0.8 and r_π = r_y = 1.78):

(24)

4. Strict nominal GDP targeting (where r_π and r_y are arbitrarily large to approximate r_π, r_y → ∞)³⁰:

(25)

5. Difference rules (where ρ = 0.8 and r_y = 0.5; two versions of this rule are tested with r_π = 1.5 and r_π = 2.5; the latter is referred to as the stricter difference rule):

(26)

6. Inflation targeting (where ρ = 0.8 and r_π = 1.5)³¹:

(27)

Welfare effects under the various policy feedback rules are contrasted in two main ways. First, impulse responses are simulated in response to a one-standard-deviation exogenous shock for all seven disturbances. We used this approach because there is no reason, ex ante, to assume that all rules respond to all shocks in equivalent manners. Some rules may work better in response to productivity shocks, some in response to spending shocks, and so on. For each shock, the squared deviation from steady state is added across horizons from 1 through 40 quarters (10 years) and presented for each of the four key macroeconomic variables: output growth, output gap, inflation, and the policy rate. Since current stabilization is preferable to future stabilization, impulse responses from every subsequent quarter are discounted at the rate β = 0.99. The comparison of squared and summed impulse responses to key variables demonstrates the ability of various policy rules to respond to each shock in isolation.

Next, we analyzed aggregate welfare effects by conducting simulations. Under each of the policy rules listed above, we have generated 10,000 series. Within each series, we have generated 10,000 observations that correspond to time periods, keeping only the final 1,000 observations/​periods. Under such simulations, the economy is affected by multiple new and lingering shocks in each period to simulate an alternate US economic history. To avoid biasing the results, we have generated multiple series. Each series, with its 1,000 retained observations, provides a standard deviation of output growth, output gap, inflation, and the policy rate. Consequently, under each policy rule, we have 10,000 estimates of the standard deviation for four key macro variables, providing a distribution of the deviations themselves. We have reported the mean as well as the 10th and 90th percentiles of these distributions in the proceeding section.

To begin, we compared the performance of the various policy regimes in response to each of the seven structural shocks from the SW2007 model (see the “Methodology” section). The seven shocks can be subcategorized into demand, supply, and monetary policy shocks. These categorizations are conducted similarly to the original SW2007 paper, where shocks that make output and inflation move in the same direction are labeled demand, shocks that make output and inflation move in opposite directions are labeled supply, and the shock appended to the monetary policy rule is labeled a monetary policy or Fed shock. For ease of comparison, impulse responses are aggregated as output measure (either output growth or output gap) + inflation + policy rate so that overall welfare losses can be measured. These sums of squared errors are presented in Table 4. The upper panel (panel A) provides results using output growth + inflation + the policy rate, and the lower panel (panel B) provides results using output gap + inflation + the policy rate. Fully disaggregated results (by each macro variable) are available in Table A1 of the Appendix.

It is immediately clear that the choice of model and the inclusion of the policy rate are both important. Different rules work well or poorly across various shocks, and no one policy rule dominates the others. Such determinations are lost when using simple models with a limited number of random fluctuations and model channels. Additionally, including the policy rate significantly alters the performance of policy rules. For instance, while strict nominal GDP targeting does well at restricting any movements in output growth and inflation, it is clearly the least desirable and most impractical rule because it requires massive changes to the policy rate. (We disregard strict nominal GDP targeting from the discussion of findings below as it primarily serves as a motivating factor for including the policy rate in welfare considerations.)

The first three result columns in Table 4 show the performance of the various policy rules for demand shocks. For these shocks, most rules perform similarly in response to a risk-premium shock (η). Still, the standard Taylor rule performs best for both the output growth and output gap, and it does so by a wider margin in the latter case. Naturally, this is because the standard Taylor rule responds directly to the output gap and does so with a large weight.

All the policy rules perform almost identically in response to exogenous spending shocks (η). However, as the results in panel B demonstrate, the output gap inclusion increases the disparity in performance among the rules and, again, the Taylor rule outperforms the others. Finally, the policy rules have a much broader disparity of outcomes when responding to investment-specific shocks (η), and the Taylor rule performs much better under both growth and gap metrics. The Taylor rule has greater performance because such shocks have a large effect on the price of capital, which in turn leads to changes in firms’ markups and requires price adjustments. However, in the “potential” economy, where no pricing frictions exist, such shocks have minor effects. As a result, the output gap—which measures the difference between the real and potential economy—is significantly affected, but output growth is not. Rules that do not weigh output metrics or weigh them weakly perform the worst, such as inflation targeting and the weaker difference rule.

Next, we considered supply shocks. Recall that shocks are characterized as affecting supply if they cause opposite movements in output and inflation.³² The three such shocks in this model affect productivity, price markups, and wage markups. For productivity shocks (η), rules targeting output growth, such as BH2019 or difference rules, improve output growth welfare, while rules targeting the output gap, such as the Taylor rule or SW2007, perform better for output gap welfare. The difference in stabilization is much stronger when using the output gap for welfare. This is because the transition of a productivity shock is relatively smooth and does not cause drastic changes in output growth.³³ While the real and potential economies converge quite quickly, a productivity shock opens a large output gap in the short run. Since short-run stabilization is more important owing to discounted future outcomes, rules that respond to this gap tend to fare better than others that consistently target output growth.

So far, the standard Taylor rule has consistently outperformed all others. However, it is not universally optimal—the Taylor rule has some drastic failures when responding to price markup (η) and wage markup (η) shocks, the latter being the most important shock in the model.³⁴ Such supply shocks only affect the real economy and not the potential economy, as nominal rigidities exist only in the real economy. As a result, the difference between the two economies, measured by the output gap, is large under these supply shocks. The Taylor rule fixates on the output gap and aims to bring it under control at the cost of increased instability for output growth, inflation, and the policy rate. This trade-off results in a substantially decreased output gap and even makes the Taylor rule optimal for price markup shocks. However, to a policymaker who cares equally about other macro variables, such a trade-off may be undesirable. Nominal GDP targeting from BH2019 performs quite well under such scenarios. It can mimic some of the stronger output responses by simply increasing the coefficient on output growth compared with most other rules, but inflation and the policy rates are kept on a more stable path due to the smoother transitions of output growth.

Using output growth, most rules are relatively similar under monetary policy shocks (η). Using the output gap, there is some variation but in an expected manner. Rules that require the Fed to weigh macro indicators heavily lower the effect of monetary shocks. Strict nominal GDP targeting is an extreme example where the Fed focuses on macro instability to an infinite degree. As a result, monetary shocks play no role. Similar but less drastic results are achieved through the standard Taylor rule. Inflation targeting and the weak difference rule perform the worst because they place low or zero weights on output, making monetary shocks more important.

Overall, the SW2007, BH2019, and difference (2.5,0.5) rules all perform similarly well at welfare stabilization (with output growth), but the standard Taylor rule performs the best when output growth is replaced by the output gap. Inflation targeting and weak difference rules perform poorly as they do not place enough emphasis on output fluctuations. But ultimately, picking a rule would require an analysis of the overall economy with multiple shocks in effect at once.

Table 5 presents the results from the simulation analysis. Recall that this analysis generates a simulated series of hypothetical US economies and computes a distribution of standard deviations for each key macro series under various policy regimes. The key series, located across the top row of Table 5, are output growth (Δy_t), output gap (x_t), inflation (π_t), and the policy rate (r_t). Having the Fed instantaneously fix nominal GDP to trend (strict nominal GDP targeting) leads to low deviations for output growth (0.43) and inflation (0.43). However, this stabilization causes unstable policy rates (3.31). Strict nominal GDP targeting requires the Fed to execute drastic changes that result in extreme rate volatility, with an increase of one order of magnitude in policy rate deviations. Both difference rules have similar deviations, but the stricter difference rule offers benefits across all variables. Therefore, we will discard strict nominal GDP targeting and the weaker difference rules from further discussions.

Among the remaining rules, it is remarkably hard to determine which one is the most desirable. Ultimately, the optimal rule choice depends heavily on which macro variable or combination of macro variables matters most to the policymaker. This would require a policymaker to specify how it comparatively weighs these different variables within a welfare function. Traditionally, inflation is weighted more than output metrics or the interest rate, but there is no academic consensus on such weights. We have followed BH2019, which weighs the output gap and inflation equally, and we remain agnostic about the relative importance of these variables—that is, we value all four variables equally. There is no clear winner across the board, and in the style of a true economics conundrum, each rule offers several distinct costs and benefits.

As the first column in Table 5 shows, output growth deviation remains similar across all rules, with barely any dramatic improvements or failures. BH2019 performs the best (0.81), while inflation targeting performs the worst (1.16). The next column shows that the standard Taylor rule outperforms all others in stabilizing the output gap. It also has a substantial advantage over the other rules—it produces an output gap deviation of only 2.16; the next best rule, SW2007, produces a deviation of 3.85. This is because the standard Taylor rule responds to the output gap itself instead of output growth. SW2007 also responds to the output gap, but the estimated coefficient in the model is very small, meaning the Fed weights the output gap minimally in its responses. As discussed earlier in this section, impulse responses to gap-targeting and growth-targeting rules are similar in most cases except for markup shocks. This is because such shocks affect the real economy but not the potential economy, causing a large change to the output gap while keeping output growth relatively unaffected. Policy rules that respond only to growth when the economy is subject to such supply shocks cause a muted policy response. Unsurprisingly, inflation targeting performs the worst at output gap stabilization (4.91). However, its deviation is still similar to that of the other rules, including the stricter difference rule, which has output growth and gap metrics of 1.02 and 4.60, respectively. This finding suggests that the Fed can still check major output fluctuations through indirect channels within the model even if it is not explicitly altering the policy rate in response to output.

It might be tempting to declare a victor, given that the standard Taylor rule clearly outperforms other rules at stabilizing the output gap. However, as the two columns farthest to the right in Table 5 demonstrate, this improvement comes at the cost of increased inflation (1.80) and policy rate (1.71) volatility—both of which are the highest among the rules being considered (disregarding strict nominal GDP targeting). Under a standard Taylor rule, the central bank is much more concerned about output gap fluctuations. Consequently, it is willing to allow increased deviations in inflation from its trend, and it is willing to alter the policy rate more frequently or aggressively.

With respect to stabilizing inflation, aside from the standard Taylor rule, most other rules are relatively similar. The difference rule performs the best (0.36) and even outperforms pure inflation targeting (0.43). SW2007 (0.54) and BH2019 (0.61) are slightly worse. The policy rate is most stable under the difference rule (0.52) and inflation targeting (0.54), and the standard Taylor rule is the worst at stabilizing the policy rate (again, disregarding strict nominal GDP targeting). SW2007 and BH2019 rank in the middle, with deviations of 0.59 and 0.69, respectively.

The standard Taylor rule is the best at stabilizing the output gap—the most difficult variable to stabilize—but at the expense of unstable inflation and interest rates. The difference rules and the pure inflation targeting rule can stabilize inflation and the policy rate fairly well, but they allow output to fluctuate much more. Rules from SW2007 and BH2019 are neither the best nor worst across the board and offer a more balanced approach to stabilization. When averaging across the standard deviations of the macro variables for each rule (keeping strict nominal GDP targeting and the weaker difference rule aside), the policy rules are ranked as follows: SW2007 (1.48), BH2019 (1.51), stricter difference rule (1.62), standard Taylor rule (1.64), and inflation targeting (1.76).

These findings demonstrate that average deviations are remarkably similar across rules. Of course, the final choice of a rule should also weigh the stabilization analysis from this section against the informational burdens associated with each rule. For instance, low output gap volatility (and therefore low unemployment volatility) may convince the Fed to adopt the standard Taylor rule, but the Fed’s forecast errors for the output gap are nonstationary. Nominal GDP targeting offers good stabilization across variables but suffers from large forecast errors. Or the Fed may wish to adopt a simple inflation targeting rule, as its forecasts of PGDP are relatively accurate and stationary. However, this choice would come at a cost to output stability. Ultimately, the expected performances of the respective rules are similar enough that debates over which rule the Fed follows should not take precedence over whether the Fed should commit to a rule. Though committing to a rule would provide the public with more certainty regarding the Fed’s actions, the expected macroeconomic effects from following the respective rules are not very different.

Monetary economists have long advocated for improving macroeconomic outcomes by minimizing the discretion of central banks in their monetary policy through the use of established rules. Unsurprisingly, few central bankers want a strict policy rule that prevents them from changing their policy stance if unforeseen circumstances arise. It is possible, though, to establish rules-based monetary policy without unduly restricting the central bank’s ability to make decisions.

For example, the approach adopted in the 2015 FORM Act would have required the Fed to use a policy reference rule. Under this approach, the Fed would commit to following its own preferred policy rule—the reference rule—unless it believed it needed to suspend the rule, and it would have to explain this decision to Congress before acting on it. Thus, this approach does not tie the Fed’s hands by making it abide by one rigid rule. It simply requires the Fed to provide concrete justification for deviations, thus leaving the public better informed.

Currently, the Fed is required to promote both price stability and low unemployment, but it has no binding requirements. Many central bankers argue that this kind of discretionary monetary policy is necessary because of the enormous complexity of the economy and its ever-changing nature. But the nature of the economy makes the case for rules-based policy. Since no one person (or small group of central bankers) can be expected to understand and react properly or consistently to changing economic conditions, the Fed should reduce uncertainty among citizens and firms by being more predictable and explaining its policy actions.

Still, we should not expect the Fed to successfully manage the economy by consistently reaching precise macroeconomic goals. A central bank is ill-suited to this sort of management of the economy. Instead, Congress should require the Fed to adopt a rules-based monetary policy to reduce uncertainty by anchoring people’s expectations regarding what the Fed will do on an ongoing basis.

This paper shows that, as with most economic decisions, any rule the Fed eventually adopts will require it to contend with trade-offs. No one rule offers both the best information advantages and macroeconomic stabilization. Nor is any one rule the best at stabilizing all variables under all shocks. Debates over which of these rules the Fed should follow must not stand in the way of Congress requiring the Fed to conduct rules-based monetary policy.

The authors thank Jerome Famularo for his excellent research assistance in preparing this document. We also thank George Selgin and the rest of the Cato Institute’s Center for Monetary and Financial Alternatives for their invaluable guidance and feedback.

Kedia, Jai, and Norbert Michel. “A Comprehensive Evaluation of Policy Rate Feedback Rules,” Policy Analysis no. 987, Cato Institute, Washington, DC, January 14, 2025.