Ten years after the financial crisis there is a new appreciation for the role household debt and financial fragility play in the business cycle. Though some economists recognized their importance going into the crisis, many observers did not and were blindsided by the severity of the Great Recession. Motivated by this experience, a spate of research over the past decade has refocused attention on the impact household balance sheets and the financial system have on the economy.
While the household balance sheet and financial panic views are distinct, they are also interrelated: household deleveraging affected the health of financial firms during the crisis while the reduction in credit supply exacerbated household financial problems. Along these lines, Gertler and Gilchrist (2018) and Aikman et al. (2018) show both factors were jointly important to the emergence of the Great Recession.3 Jordà, Schularick, and Taylor (2013, 2015, 2016), relatedly, in their cross-country studies find countries with high household debt levels tend to have a higher incidence of financial crises. Highly leveraged household sectors and financial crises, in other words, are often a jointly determined process.
This new appreciation for household debt and financial fragility can be seen from a broader perspective as the long-time coming consequence of the advanced economies credit regime that emerged in the 1980s. Jordà, Schularick, and Taylor (2017) show that private sector credit growth relative to GDP accelerated during that decade, creating a “financial hockey stick” pattern of leverage for advanced economies. They show this development has dampened business cycle volatility overall while making advanced economies more susceptible to spectacular financial crashes.
This renewed interest in household balance sheets and financial system stability has led to several different policy recommendations. First, the IMF, BIS, and policymakers in many advanced economies have called for macroprudential regulation. This approach focuses on the stability of the entire financial system and works by adjusting buffers — such as countercyclical capital requirements and caps on loan to value ratios — to respond to aggregate financial shocks.
This approach, however, is not without its challenges. It is hard to know what is a true financial vulnerability, what are the appropriate indicators to follow, and how to define financial stability.4 In addition to these knowledge problems, macroprudential goals may conflict with other policy goals and be subject to rent seeking by affected parties.5 For these reasons, macroprudential regulations, which have been implemented to varying degrees in different countries, are not yet fulfilling all of their desired goals (IMF 2018; BIS 2018).
A second policy recommendation put forth by some observers is the need for state-contingent debt contracts (Shiller 2008; Mian and Sufi 2014; Eberly and Krishnamurthy 2014; Piskorski and Seru 2018). These are financial contracts whose payouts are contingent on certain economic outcomes. In this context, the push has been for mortgages whose principal and payments are indexed to local economic conditions. A weakening local economy would lower the real mortgage burden on households while a booming one would raise it. Such mortgages would resemble equity more than debt and lead to better risk sharing between debtors and creditors. In turn, this improved distribution of risk should improve the stability of the financial system. Shiller (2004), more generally, shows how these and other state-contingent contracts could radically transform our world into a more equitable and flourishing place.
Some progress has been made on this front with income-contingent student loans, contingent convertible corporate bonds, and a few state-contingent mortgages.6 Most debt, however, remains written in fixed nominal terms. The dearth of contingent debt contracts suggests that the cost of writing and enforcing them is prohibitively expensive. For now, then, state-contingent contracts do not provide a practical solution to the household debt and financial stability concerns of advanced economies.
A third policy recommendation that addresses these concerns is to use monetary policy to create better risk sharing between debtors and creditors. Specifically, a monetary regime that targets the growth path of nominal GDP (NGDP) can be shown to reproduce the distribution of risk that would exist if there were widespread use of state-contingent debt securities (Koenig 2013; Sheedy 2014; Azariadis et al. 2016; Bullard and DiCecio 2018). The basic idea is that the countercyclical inflation created by an NGDP target will cause real debt burdens to change in a procyclical manner. As a result, debtors will benefit during recessions and creditors will benefit during booms. Fixed nominal-priced loans will act more like equity than debt and therefore promote financial stability.
This policy recommendation has the potential to be the most tractable of the above three proposals since it only requires a NGDP-targeting monetary regime. While switching to such a monetary regime is a nontrivial task, it would accomplish the same goals of state-contingent debt contracts and complement the efforts of macroprudential regulations. However, of the three proposals this one has received the least attention. This may be due to the fact that the recent work on this proposal been largely theoretical since no country explicitly targets NGDP. This policy proposal, consequently, is ripe for further attention and development.
This article attempts to shed more light on this proposal by providing the first empirical assessment of it. It does so by exploiting an implication of the theory: those countries whose NGDP stayed closest to its expected precrisis growth path during the crisis should have experienced the least financial instability. Put differently, some countries experienced more stability in aggregate nominal spending than others and these differences should be systematically related to financial stability if the theory is true. So even though no countries were targeting NGDP during the crisis, there is still a way to test the theory.
This article uses this understanding to provide an empirical test of the third policy proposal. It does so by outlining a method for estimating the expected growth path of NGDP for advanced economies and then seeing whether the gap between it and actual NGDP is systematically related to various measures of financial stability. This exercise is only a first look and is not the final word, but the results indicate more attention should be given to this third proposal. The findings strongly suggest that a stable NGDP growth path supports financial stability. These findings, therefore, lend support to the existing arguments for why advanced economies should consider adopting an NGDP level target.
In the sections that follow, the article further outlines the arguments of Koenig (2013), Sheedy (2014), Azariadis et al. (2016), and Bullard and DiCecio (2018). It then derives the expected growth path of NGDP for 21 advanced economies using IMF data and the “sticky forecast” approach of Beckworth (2018). Next, the article uses this measure to create an NGDP gap that is used in some scatterplots, a panel vector autoregression, and a panel local projection model to determine the relationship between the NGDP gap and various economic variables. The article then concludes with some policy considerations.
Better Risk Sharing through NGDP Targeting
The key insight of Koenig (2013), Sheedy (2014), Azariadis et al. (2016), and Bullard and DiCecio (2018) is that in a world of incomplete markets where there is nonstate contingent nominal contracting, an NGDP target can reproduce the risk distribution that would occur if there were complete markets and state contingent nominal debt contracting.7 An NGDP target, in other words, can make up for the lack of insurance against future risks that could affect debtors’ ability to repay their debts. Conversely, an NGDP target can also make up for the lack of insurance against potential returns creditors might miss out on because their funds are locked up in fixed-price nominal loans. Bullard and DiCecio (2018) show that this result holds even when the modeled heterogeneity among debtors and creditors approximates that of the actual income, financial wealth, and consumption inequality in the United States. They note this makes NGDP targeting “monetary policy for the masses.”
The intuition behind these formal findings is that debtors and creditors who have committed to fix-nominal debt contracts and therefore to fixed money payments can be subject to both price level and real income shocks. The former shocks have long been understood and generally seen as bolstering the case for a price-level or inflation target. Most famously, Irving Fisher (1933) made the case for price level stability as a way to avoid unexpected deflation and a rise in real debt burdens that could trigger a cascade of loan defaults. As Koenig (2013) notes, however, Fisher’s “debt deflation” scenario is incomplete because it only looks at price level shocks. Debtors may also face financial stress from negative real income shocks. Both types of shocks make it harder for debtors to service fixed money payments since both shocks lower nominal income flows relative to expectations. In both cases, the debtor is bearing the additional risk of these negative shocks relative to the creditor.
These two scenarios are illustrated in Table 1 as (1) and (2), where Δpt, Δyt, and Δ(py)t represent changes in the log of the price level, real income, and nominal income. Note, that in general, any combination of these shocks that lowers nominal income relative to expectations puts a strain on debtors. It follows, then, that stabilizing Δ(py)t via an NGDP target serves a useful insurance function for debtors. For a central bank, that means allowing changes in price level to offset real income shocks so that actual nominal income equals expected nominal income. That is, in order for the following nominal income equality to hold
it must be the case that innovations to real income be offset by innovations to the price level:
or, equivalently:
Another way to understand equation (3) is that under an NGDP target a negative real income shock leads to an unexpectedly higher price level and, for a given stock of fixed-price nominal debt, an unanticipated lower real debt burden for the debtor. The creditor, consequently, receives a lower real debt payment than expected and shares in the real income loss. In short, the risk of a real income loss is shared more evenly between the debtor and creditor under an NGDP target than under a price stability target.
Equation (3) also implies that under an NGDP target a positive real income shock will lead to an unexpectedly lower price level and, for a given stock of fixed-price nominal debt, an unanticipated higher real debt payment from the debtor to the creditor. This feature can be seen as providing insurance to a creditor against having their funds locked up in a fixed nominal loan with a constant yield while real earnings in the rest of the economy rise due to the positive real income shock.
Imagine, for example, there is a positive total factor productivity (TFP) shock that raises real returns in the economy. If a creditor knew this productivity innovation was going to occur ex-ante, he would have required an equivalent risk-adjusted return on a loan to a debtor. But the creditor cannot know this outcome ex-ante since it is a shock. Under a price stability target, the creditor bears this risk and would miss out on the gain from the TFP shock. An NGDP target, on the other hand, forces the debtor to share some of the “windfall gain” with the creditor through a higher real debt payment. Again, risk is shared more evenly between the debtor and creditor under the NGDP target and therefore mimics a world of state-contingent debt contracts.
Finally, if there are no real income shocks then an NGDP target effectively defaults to a price stability target so that Δpt = ΔptEt−1.8 An NGDP target, consequently, also avoids the “bad” price level surprises depicted in scenarios (1) and (3) in Table 1.9
In practice, a central bank targeting NGDP does not need to manually adjust the price level to offset real income shocks. Instead, the central bank simply aims to keep aggregate nominal spending on its targeted growth path and the price level will by default adjust to the real income shocks. The insurance benefits from the countercyclical inflation are therefore produced automatically (Beckworth 2017).
No central bank has ever attempted a NGDP target, but the Bank of Israel (BoI) has unintentionally provided an example of what such a monetary regime might look like. The BoI officially targets an inflation range of 1–3 percent, but as Figure 1 shows, NGDP in Israel has been growing on a fairly stable trend since 2008. As a consequence, real income shocks have led to almost mirror opposite movements in the inflation rate as measured by the GDP deflator. This inverse relationship is not perfect, but it is strong enough that the GDP deflator inflation has been allowed to temporarily move outside the inflation target range when there have been large real income shocks. For example, in 2009 during the Great Recession the inflation rate just topped 5 percent. Despite this inflation flexibility, inflation on average over the entire period in Figure 1 has been near the center of its targeted range at a rate of 1.9 percent. An explicit NGDP target would arguably result in a similar outcome.
Measuring NGDP Expectations
The main objective of this paper is to empirically assess the policy proposal that NGDP targeting will result in better risk sharing between debtors and creditors. An obvious challenge to doing so is that no country has targeted NGDP so there is no track record to evaluate.10
There is, however, an indirect way to test this proposal by exploiting an implication of the theory. It predicts that those countries whose NGDP stayed closest to its expected precrisis growth path should have experienced the least financial instability during the crisis. Put differently, some countries experienced more stability in aggregate nominal spending than others during the crisis and these differences should be systematically related to financial stability if the theory is true. A cross-country sample over this period of NGDP deviations from expected growth paths should reveal whether this prediction is borne out in the data.
This possibility raises another challenge: how best to measure the expected growth path of NGDP? One wants to avoid using simple, naïve precrisis trends since expectations and nominal contracting do eventually adjust. Figure 2 illustrates the problem with such trends for the United States and Spain. If they were taken seriously, then there would be a 15 percent shortfall of aggregate nominal expenditures in the United States and a 45 percent shortfall in Spain as of 2018:Q2. Figure 2 reports another measure, the “sticky forecast” path of NGDP outlined in Beckworth (2018) and it shows a gradual adjustment so that the expected path of NGDP and actual NGDP eventually converge. This measure is more consistent with the notion of expectations and nominal contracting eventually adjusting to sustained changes in NGDP. This sticky forecast is used in this paper as the expected growth path of NGDP for 21 advanced economies and its motivation and construction is outlined below.
Sticky Forecast Path for NGDP
The idea behind the sticky forecast path for NGDP is twofold. First, the public makes many economic decisions based on a forecast of their nominal incomes. For example, households may take out a 30-year mortgage based on an implicit forecast of their nominal income over this horizon. The actual realization of nominal income may turn out to be very different than expected, but the households may not be able to quickly adjust their plans given sticky debt contracts and other commitments that constrain them. Therefore, the consequences of previous forecasts are often binding on them and slow to change even if their nominal income forecasts have been updated. Second, in addition to these old forecasts and decisions whose influence lingers, new forecasts and new decisions are being made each quarter for subsequent periods that will also have lingering effects. Together, this means future periods have many overlapping and different forecasts applied to them that only gradually adjust.
To capture this sticky forecast idea, a five-year forecast is created that gradually updates over time. Five years are chosen since it is assumed that all constraints created by decisions based on the forecast can be fully unwound within five years. The data for this exercise come from the IMF’s World Economic Outlook (WEO) forecast database. Every spring and fall there are WEO forecasts published for member countries that extend six years out. These biannual forecasts are interpolated to a quarterly frequency and used here to construct a sequence of five-year overlapping forecasts for every period between 2000:Q1 to 2018:Q2. This process is done for 21 advanced economies: Australia, Austria, Belgium, Canada, Denmark, Finland, France, Germany, Greece, Israel, Italy, Japan, Netherlands, New Zealand, Portugal, South Korea, Spain, Sweden, Switzerland, United Kingdom, and the United States.11
The exact steps are as follows. First, for every quarter beginning in 1995, a five-year forecast (20 quarters) is created using the IMF’s forecasts of NGDP growth.12 Second, for a given starting period, these NGDP growth forecasts are then used to create a 20-quarter forecast path of the NGDP level in national currency form. These forecasts are created for every period up to 2008:Q2.
Third, the next step is to recognize that starting with 2000:Q1 there are 20 overlapping NGDP level forecasts in national currency for every quarter. All of these 20 forecasts are averaged into one NGDP level value for each period as follows:
This process is repeated for every forecasted period so that a new NGDP level forecast time series is created. This new time series is used as the sticky forecast NGDP growth path. Figure 3 shows the actual and sticky forecast paths for NGDP in the 21 advanced economies in their national currency. There is a diverse set of NGDP experiences in Figure 3, but it is misleading to compare across countries the actual and sticky forecast NGDP levels since absolute size matters. This paper, consequently, looks at the percentage point difference between the actual and sticky forecast NGDP levels, called hereafter the “NGDP Gap.”
Figure 4 reports the average NGDP gap for the crisis years of 2008:Q1–2013:Q4 ranked by size. Most countries had a negative NGDP gap during this time, indicating NGDP was on average below expected values in most advanced economies. Greece had the largest average NGDP gap at −14.9 percent, followed by Spain at −8.7 percent and Portugal at −6.5 percent. The best performers turned out to be Israel and Australia both with an NGDP gap of 1.6 percent followed by Switzerland at 0.2 percent. The risk sharing theory of NGDP outlined by Koenig (2013), Sheedy (2014), Azariadis et al. (2016), and Bullard and DiCecio (2018) implies these NGDP Gap differences among the 21 countries should be systematically related to financial stability. This claim is tested in the next section.
Empirical Evidence for NGDP and Financial Stability
This section gets to the main objective of this article: to empirically assess the policy proposal to use NGDP as a way to improve financial stability. As noted earlier, it does so by exploiting an implication of the theory: those countries whose NGDP stayed closest to its expected precrisis growth path — and therefore kept risk more evenly spread between debtors and creditors — should have experienced the least financial instability. This section of the article tests this claim in two parts. First, it looks at series of scatterplots to see if there is any systematic relationship between the NGDP gap and measures of financial stability. Second, it then uses the same variables in a panel vector autoregression (VAR) and panel local projection model to better test for causality.
Scatterplot Analysis
As a first look at the potential relationship between NGDP and financial stability, this section plots in Figure 5 the average NGDP gap over the crisis period of 2008:Q1–2013:Q4 against six financial measures over the same period: private credit growth, M3 money supply growth, stock price growth, home price growth, the nonperforming loan (NPL) rate, and the equity risk premium. Details on the sources of these measures are found in the data appendix. To be clear, these scatterplots are not intended to establish causality. Instead, they are provided to establish whether there is any systematic relationship between NGDP forecasting errors and the financial variables.
One issue is whether to treat Greece as a legitimate observation or an outlier given the severity of its experience during this time. On one hand, Greece can be viewed as part of the same data-generating process as other countries but it just happened to receive the largest “treatment” of NGDP forecasting errors. In this case, including Greece is important since its absence could result in biased estimates. On the other hand, maybe Greece does come from a different data-generating process and should be considered an outlier. To account for this possibility, the scatterplots are shown with fitted lines and R2 for the full sample and for the sample excluding Greece.
The first scatterplot in the figure shows the change in the average year-over-year growth rate of credit to the private nonfinancial sector (PNFS) against the NGDP gap. The change is the difference between the average PNFS credit growth rate in 2003:Q1–2007:Q4 and in 2008:Q1–2013:Q4. That is, the change in the average credit growth rate between the boom and crisis years. The first scatterplot shows there is a fairly strong and positive relationship with an R2 of 48 percent when all countries are included. Without Greece, the R2 is still a robust 38 percent. These results mean the larger the decline in the NGDP gap, the greater the decline in the average growth rate of PNFS credit during the crisis years.
The second scatterplot reveals a similar positive relationship for the year-over-year M3 money supply growth rate. Here the R2 is 58 percent for the full sample and 56 percent without Greece. Here too, then, the figure indicates a strong positive relationship between the NGDP gap and the growth in the M3 money supply.
The third scatterplot displays the relationship between the year-over-year growth rate in stock prices and the NGDP gap. Here again, there is a strong positive relationship between the size of the NGDP gap and the growth in stock prices in the full sample with an R2 of 54 percent. The relationship weakens a bit, but remains nontrivial in size with an R2 of 23 percent in the absence of Greece. In general, the larger the decline in the NGPD gap the greater the decline in this asset price.
The fourth scatterplot shows the relationship between the year-over-year growth in home prices and the NGDP gap. This relationship is also a strong positive one with an R2 of 64 percent for the full sample. Excluding Greece actually leads to a stronger fit with an R2 of 69 percent. This is another asset price that is strongly related to the NGDP gap during the crisis.
The fifth scatterplot reveals the relationship between nonperforming loans as a percent of gross loans against the NGDP gap. Now there is a strong negative relationship, indicating that as the NGDP gap declines the rate of nonperforming loans increases. The R2 here is 61 percent for the full sample and 30 percent excluding Greece. Nonperforming loans also appear to be robustly related to the NGDP gap.
Finally, the sixth scatterplot displays the relationship between the equity risk premium and the NGDP gap. Here, there is a strong negative relationship for the full sample with an R2 of 56 percent, indicating that as the NGDP gap gets larger the equity risk premium rises. The R2, however, shrinks to 10 percent when Greece is excluded. This may be the one case where Greece is an outlier.
Figure 6 shows the NGDP gap was also systematically related to year-over-year real GDP growth and the unemployment rate during this time. It was less related, however, to the year-on-year inflation rate. There is a stronger fit, though, between the NGDP gap and the change in trend inflation between the 2008–2013 and 2003–2007 periods.
These scatterplots, therefore, indicate that in most cases there was a strong systematic relationship between the NGDP gap and financial and economic instability. Moreover, since most countries experienced persistent NGDP forecast errors during this period, one can view macroeconomic policy as failing to provide on a sustained basis sufficient nominal demand growth and therefore was an exogenous contributor to this relationship. Put differently, it seems plausible that a meaningful portion of causality flowed from NGDP forecast errors to financial variables in these scatterplots. Still, the scatterplots only establish a relationship. The next section attempts to establish causality.
Panel VAR
To better tease out causality, this section estimates a panel vector autoregression. A VAR is an estimated system of endogenous variables that provides a dynamic forecast. The forecast can be used to identify nonforecasted movements or innovations to variables in the system. These innovations coupled with identification restrictions on the data create exogenously identified shocks to variables of interest. Here, that variable of interest is the NGDP gap.
The VAR is estimated on the data for all 21 countries using quarterly data over the entire sample of 2000:Q1 to 2018:Q2. This larger sample is used to avoid degrees of freedom problems that arise using the shorter sample period of the crisis. Moreover, the theory applies to boom periods as much as it does to bust periods since any deviation of NGDP from its expected growth path should affect the distribution of risk between debtors and creditors.
Since this is panel data, a panel VAR is estimated that controls for individual country fixed-effects. This feature means unobserved country-specific heterogeneity that is fixed over the sample will not affect the estimates. Greece, therefore, should not be a problem for these estimates.
A parsimonious panel VAR is estimated that has three core macroeconomic variables — the NGDP gap, real GDP growth, and the unemployment rate — and a financial variable as its endogenous variables:
Here, zi,t is the vector of endogenous variables, 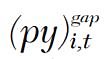 is the NGDP gap, Δyi,t is the year-over-year growth rate in real GDP, ui,t is the unemployment rate, and fi,t is one of the six financial variables. The subscripts i and t and represent country i and time period t. This model is estimated six times with a separate financial variable filling the fi,t slot each time. The model is also estimated an additional time with inflation filling the fi,t slot.13 Four lags are used in the estimated model and a Choleski identification scheme is imposed on the data.
is the NGDP gap, Δyi,t is the year-over-year growth rate in real GDP, ui,t is the unemployment rate, and fi,t is one of the six financial variables. The subscripts i and t and represent country i and time period t. This model is estimated six times with a separate financial variable filling the fi,t slot each time. The model is also estimated an additional time with inflation filling the fi,t slot.13 Four lags are used in the estimated model and a Choleski identification scheme is imposed on the data.
Given the ordering of the variables, the Choleski identification means the 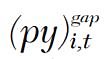 shock is exogenous to all other variables in the short-run. This allows for impulse response functions (IRFs), which show the typical dynamic response of the variables in the VAR to an exogenous shock to the NGDP gap. The shock to the NGDP gap is set to a negative 1 unit shock. The resulting IRFs are reported in Figure 7.
shock is exogenous to all other variables in the short-run. This allows for impulse response functions (IRFs), which show the typical dynamic response of the variables in the VAR to an exogenous shock to the NGDP gap. The shock to the NGDP gap is set to a negative 1 unit shock. The resulting IRFs are reported in Figure 7.
The top row of Figure 7 shows the IRFs for the credit to the private nonfinancial sector and the M3 money supply both in year-over-year growth rate form. The negative 1 unit shock to the NGDP gap causes both to respond in a similar fashion: they slowly decline for nine quarters and then slowly begin recovering. They are still recovering 14 quarters after the shock. The maximum decline in the private credit growth rate is 0.94 percent and for the M3 growth rate it is 0.89 percent.
The second row of Figure 7 reveals the IRFs for stock and home price year-over-year growth rates. The stock price growth rate declines through three quarters and hits a peak decline of 3.9 percent. The home price growth rate stays depressed over the entire IRF and averages a 0.58 percent decline.
The third row of Figure 7 displays the IRFs for the nonperforming loan rate and the equity risk premium. They both slowly rise over the entire IRF. The nonperforming loan rate tops out at 0.49 percent and the equity risk premium reaches 0.57 percent. Unlike the scatterplots, the equity risk premium remains significant in the IRFs.
The last two rows of Figure 7 show the response of the macroeconomic variables. The real GDP growth rate declines to about −1 percent through quarter four and then recovers relatively quickly. The unemployment rate, on the other hand, rises through quarter eight, peaking with a 0.57 percent gain, and begins a slow recovery. The inflation IRF indicates there is no link between it and the NGDP gap shock. This is consistent with the weak relationship in scatterplots and may reflect the successful anchoring of inflation by central banks. Finally, the NGDP gap is shown to start recovering in quarter three from its own shock.
The panel VAR IRFs, therefore, collectively point to a strong causal role for NGDP shocks in creating financial and economic instability. These findings, therefore, provide empirical support for the proposal to use NGDP targeting as a means to deal with concerns over household debt and financial volatility.
Panel Local Projection Model
One criticism of the Panel VAR is that it applies some structure to the data via the Choleski identification scheme. The data is therefore not strictly “speaking for itself.” As a cross check, then, this section reports IRFs from Jordà’s (2005) local projection method that are not subject to this critique. Moreover, the local projection method allows for nonlinearities and provides a more direct estimate of dynamic causal effects. In addition, the local projection like the VAR is applied using panel data and fixed effects so that unobserved country-specific heterogeneity is controlled for in the regressions. Greece, therefore, should not be a problem for these estimates.
The panel local projection approach entails estimating h regressions of the form,
where h is the number of quarters ahead, j is the number of lags, βi,hDi are country fixed effects, and γ,θ,π,ρ are parameter estimates on the same lagged control variables used in the panel VAR. Like before, the fi represents a placeholder for the financial and inflation variables.14 Also like before, four lags are used for J.
This panel local projection regression is estimated for all the variables for h = 0,...,14. That is, regressions at each h horizon are estimated with the parameter of interest being βh. This parameter estimates the direct effect of the NGDP gap at time t on the other variables at time t + h. Unlike the panel VAR, the local projection regression imposes no structure on the data and allows the data to speak for itself.
The lagged control variables are included to help keep βh estimates unbiased. However, in the regressions with small h there may still be some simultaneity bias. But as h gets larger it is harder to argue endogeneity is a problem.15
The local projection IRFs are created by plotting the point estimates for βh and the accompanying 95 percent clustered standard error (SE) bands. These IRFs are reported in Figure 8 for all the variables following a negative 1-unit shock to the NGDP gap.
Figure 8 reveals the local projections IRFs are very similar to the Panel VAR IRFs. The top row of Figure 8 shows the IRFs for the credit to the private nonfinancial sector growth rate and the M3 money supply growth rate similarly decline for nine quarters before slowly recovering. The magnitudes are also similar with a maximum decline in the private credit growth rate of 0.93 percent and a decline in the M3 growth rate of 0.78 percent.
The second row of Figure 8 also shows similar IRFs for stock and home price growth rates. The stock price growth rate declines through three quarters and hits a peak decline of 3.6 percent. The home price growth rate also stays depressed over the entire IRF and averages a 0.83 percent decline.
The third row of Figure 8 displays the IRFs for the nonperforming loan rate and the equity risk premium. The point estimates are again very similar to the panel VAR IRFs, though the standard error bands are much larger for the local projection IRFs.
The fourth row reveals very similar IRFs for the macroeconomic variables. Real GDP growth and the unemployment rate change by similar amounts, inflation remains insignificant, and the NGDP gap recovers rather briskly.
The local projection IRFs, therefore, tell the same story as the Panel VAR IRFs: a negative NGDP gap shock appears to causally affect the financial and macroeconomic variables in an adverse manner. Only inflation is left unscathed. Once again, then, the evidence points to a strong causal role for NGDP in promoting financial and economic stability.
Conclusion
NGDP level targeting (NGDPLT) has received increased attention over the past decade for various reasons. Some see it as the next step in the evolution of monetary policy regimes since it avoids much of the confusion inherent to inflation targeting (Frankel 2012; Beckworth 2014; Sumner 2011, 2014; Garin, Lester, and Sims 2016). Others have made the case for NGDPLT based on the desirable commitment properties its creates in the face of a zero lower bound (ZLB) environment (Woodford 2012; Summers 2018). NGDPLT can similarly be seen as a velocity-adjusted money supply target that is effective in escaping the ZLB (Belongia and Ireland 2015, 2017). Finally, some see NGDPLT as a workaround to the knowledge problem in monetary policy. There is no need to have real-time knowledge of natural-rate variables in this framework (McCallum 2011; Beckworth 2017; Beckworth and Hendrickson 2019).
These more traditional cases being made for NGDPLT can now be bolstered by the risk-sharing argument for it. That is, a monetary regime that targets the growth path of NGDP can be shown to reproduce the distribution of risk that would exist if there were widespread use of state-contingent debt securities (Koenig 2013; Sheedy 2014; Azariadis et al., 2016, Bullard and DiCecio 2018). The idea behind this view is that the countercyclical inflation created by an NGDPLT will cause real debt burdens to change in a procyclical manner. This tendency, in turn, will cause debtors to benefit during recessions and creditors to benefit during booms. Put differently, an NGDPLT will cause fixed nominal-priced loans to act more like equity than debt.
This article provided an indirect empirical assessment of this risk-sharing view of NGDP. It did so by first constructing an NGDP gap measure and checking whether it was systematically related to various measures of financial stability. The paper then used a panel VAR and a panel local projection model to determine if causality ran from NGDP shocks to financial stability. The results from these empirical exercises strongly suggest that there is a meaningful causal role for NGDP in promoting financial and economic stability.
These findings are only a first look at the NGDP–financial stability relationship. Hopefully, they will spur further research on this issue and help inform the discussion at the Federal Reserve and elsewhere on the best monetary policy regime for advanced economies.
References
Aikman, D.; Bridges, J.; Kashyap, A.; and Siegart, C. (2018) “Would Macroprudential Regulation Have Prevented the Last Crisis?” Bank of England Staff Working Paper No. 747.
Anthony, M.; Balta, N.; Best, T.; Nadeem, S.; and Togo, E. (2017) “What History Tells Us about State-Contingent Debt Instruments.” Vox CEPR Policy Portal (June 6).
Azariadis, C.; Bullard, J.; Singh, A.; and Suda, J. (2016) “Incomplete Credit Markets and Monetary Policy.” Federal Reserve Bank of St. Louis Working Paper.
Bailey, S. (1837) Money and Its Vicissitude in Value. London: Effingham Wilson.
Beckworth, D. (2014) “Inflation Targeting: A Monetary Policy Regime Whose Time Has Come and Gone.” Mercatus Policy Paper (July 10).
__________ (2017) “The Knowledge Problem in Monetary Policy: The Case for Nominal GDP Targeting.” Mercatus Policy Brief (July 18).
__________ (2018) “Nominal GDP as the Stance of Monetary Policy: A Practical Guide.” Mercatus Working Paper.
Beckworth, D., and Hendrickson, J. (2019) “Nominal GDP Targeting versus the Taylor Rule on an Even Playing Field.” Journal of Money, Credit, and Banking. Forthcoming.
Belongia, M., and Ireland, P. (2015) “A ‘Working’ Solution to the Question of Nominal GDP Targeting.” Macroeconomic Dynamics 19 (3): 508–34.
__________ (2017) “Circumventing the Zero Lower Bound with Monetary Policy Rules Based on Money.” Journal of Macroeconomics 54 (Part A, December): 42–58.
Bernanke, B. (2018) “The Real Effects of the Financial Crisis.” Brookings Papers on Economic Activity (September).
BIS (Bank for International Settlements) (2018) “Chapter IV: Moving Forward with Macroprudential Frameworks.” In BIS Annual Economic Report, 63–89.
Brunnermeier, M. K. (2009) “Deciphering the Liquidity and Credit Crunch 2007–2008.” Journal of Economic Perspectives 23 (1): 77–100.
Bullard, J., and DiCecio, R. (2018) “Optimal Monetary Policy for the Masses.” Federal Reserve Bank of St. Louis Working Paper.
Eberly, J., and Krishnamurthy, A. (2014) “Efficient Credit Polices in a Housing Crisis.” Brookings Papers on Economic Activity (Fall): 73–119.
Fisher, I. (1933) “The Debt-Deflation Theory of the Great Depression.” Econometrica 1 (4): 337–57.
Frankel, J. (2012) “Inflation Targeting Is Dead: Long-Live Nominal GDP Targeting.” VoxEU (June 19).
Garín, J.; Lester, R.; and Sims, E. (2016) “On the Desirability of Nominal GDP Targeting.” Journal of Economic Dynamics and Control 69: 21–44.
Gertler, M., and Gilchrist, S. (2018) “What Happened: Financial Factors in the Great Recession.” Journal of Economic Perspectives 32 (3): 3–30.
Gorton, G. (2012) Misunderstanding Financial Panics: Why We Don’t See Them Coming. Oxford: Oxford University Press.
Hendrickson, J. (2012) “An Overhaul of Federal Reserve Doctrine: Nominal Income and the Great Moderation.” Journal of Macroeconomics 34 (2): 304-17.
IMF (International Monetary Fund) (2018) “Chapter 2: The Global Economic Recovery 10 Years after the 2008 Financial Crisis.” In the International Monetary Fund October 2018 World Economic Report, 71–100.
Jordà, Ò. (2005) “Estimation and Inference of Impulse Responses by Local Projections.” American Economic Review 95 (1): 161–82.
Jordà, Ò.; Schularick, M., and Taylor, A. (2013) “When Credit Bites Back.” Journal of Money, Credit and Banking 45 (S2): 3–28.
__________ (2015) “Betting the House.” Journal of International Economics 96 (S1): S2–S18.
__________ (2016) “The Great Mortgaging: Housing Finance, Crises and Business Cycles.” Economic Policy 31 (85): 107–52.
__________ (2017) “Macrofinancial History and the New Business Cycle Facts.” In M. Eichenbaum and J. Parker (eds.) NBER Macroeconomics Annual Report 2016, 213–63. Chicago: University of Chicago Press.
Koenig, E. (2013) “Like a Good Neighbor: Monetary Policy, Financial Stability, and the Distribution of Risk.” International Journal of Central Banking 9 (2): 57–82.
Lombardi, M.; Mohanty, M.; and Shim, I. (2017) “The Real Effects of Household Debt in the Short and Long Run.” BIS Working Paper No. 607.
McCallum, B. (2011) “Nominal GDP Targeting.” Shadow Open Market Committee Meeting (October 21).
Mian, A.; Rao, K.; and Sufi, A. (2013) “Household Balance Sheets, Consumption, and the Economic Slump.” Quarterly Journal of Economics 128 (4): 1687–1726.
Mian, A., and Sufi, A. (2010) “Household Leverage and the Recession of 2007 to 2009.” IMF Economic Review 58 (1): 74–117.
__________ (2014) House of Debt: How They (and You) Caused the Great Recession, and How We Can Prevent It from Happening Again. Chicago: University of Chicago Press.
Mian, A.; Sufi, A.; and Verner, E. (2017) “Household Debt and Business Cycles Worldwide.” SSRN Scholarly Paper 2655804 (February 9).
Niskanen, W. (2001) “A Test of the Demand Rule.” Cato Journal 21(2): 205–9.
Piskorski, T., and Seru, A. (2018) “Mortgage Market Design: Lessons from the Great Recession.” Brookings Papers on Economic Activity 49 (1): 429–99.
Ricks, M. (2016) The Money Problem: Rethinking Financial Regulation. Chicago: University of Chicago Press.
Salter, A. (2014) “The Imprudence of Macroprudential Policy.” The Independent Review 19 (1): 5–17.
Selgin, G. (2018) Less Than Zero: The Case for a Falling Price Level in a Growing Economy, 2nd ed. Washington: Cato Institute.
Sheedy, K. (2014) “Debt and Incomplete Financial Markets.” Brookings Papers on Economic Activity 45 (1): 301–61.
Shiller, R. (2004) The New Financial Order: Risk in the 21st Century. Princeton, N.J.: Princeton University Press.
__________ (2008) The Subprime Solution: How Today’s Global Financial Crisis Happened, and What to Do About It. Princeton, N.J.: Princeton University Press.
Summers, L. (2018) “Why the Fed Needs a New Monetary Policy Framework.” In H. Summers, D. Wessel, and J. David (eds.) Rethinking the Fed’s 2 Percent Inflation Target. Washington: Brookings Institution.
Sumner, S. (2011) “Re-Targeting the Fed.” National Affairs (Fall): 79–96.
__________ (2014) “Nominal GDP Targeting: A Simple Rule to Improve Fed Performance.” Cato Journal 34 (2): 315–37.
Woodford, M. (2012) “Methods of Policy Accommodation at the Interest-Rate Lower Bound.” In Proceedings — Economic Policy Symposium — Jackson Hole, 185–288. Federal Reserve Bank of Kansas City.

Cato Journal, Vol. 39, No. 2 (Spring/Summer 2019). Copyright © Cato Institute. All rights reserved.
David Beckworth is Director of the Monetary Policy Project and a Senior Research Fellow at The Mercatus Center, George Mason University.
1 Cross-country studies similarly find that those countries with rising household debt to GDP ratios generally experience slower economic growth over the medium to long-term horizons (Mian, Sufi, and Verner 2017; Lombardi, Mohanty, and Shim 2017).
2 Cross-country analysis similarly finds that those countries with greater financial vulnerabilities leading up to the crisis experienced larger economic losses after the crisis (IMF 2018).
3 Bernanke (2018) makes the case that the severity of the Great Recession was mostly due to the financial panic.
4 For more on the knowledge problem inherent to macroprudential regulations see Salter (2014).
5 The recent delisting of Prudential as a significantly important financial institution (SIFI) by the U.S. Financial Stability Oversight Council is seen by some as an example of rent seeking.
6 Companies like Unison, Patch, and Point have begun offering state contingent-like mortgages but remain a small part of the mortgage-origination market due, in part, to government-sponsored enterprises (GSEs) subsidizing traditional mortgages. There has also been some limited use of state-contingent debt contracts by sovereigns (see Anthony et al. 2017).
7 The ideas in these formal papers date back to Bailey (1837: 111–33) as shown by Selgin (2018: 57–70).
8 This can be seen in equation (3) by noting that if there are no real income shocks then Δyt = ΔytEt−1 and Δpt = ΔptEt−1.
9 The “bad” price level surprises should be distinguished from the “good” price level surprises that an NGDP target creates when there are real income shocks. As noted above, in the latter case these price level surprises act as a form of insurance.
10 Niskanen (2001) and Hendrickson (2012) make the case that the Fed was effectively targeting a stable growth path for nominal demand during the post–Paul Volcker period up until the early 2000s. This period of stable nominal demand growth and relative financial stability lends support to the arguments of this article.
11 For South Korea and Japan, the forecast is set at 2.5 years since these two countries’ forecasts were found to converge much faster.
12 The IMF provides forecasts for real GDP growth and inflation. These are combined to create an NGDP growth forecast.
13 The impulse response functions (IRFs) of the core macroeconomic variables do not materially change with the change in the financial variables.
14 Here, fi also serves as placeholder for the core macroeconomic variables when they are run as the dependent variable. When this happens, the ρ control variables fall away since the lagged macroeconomic variables are provided in the γ,θ, and π control variables.
15 It seems implausible, for example, that the NGDP gap shock at period t — which itself is a forecast error — is caused by the year-on-year growth rate of stock prices 14 quarters in the future.
















