An alternative view supported by much of the academic literature is that natives and immigrants largely take different types of jobs, potentially because they have different comparative advantages, even among less educated workers. If so, then the native wage response to a reduced supply of immigrant workers would not be large if it existed at all. It is not difficult to find examples of occupations that native workers do not enter, such as seasonal farm labor (Clemens 2013). However, those occupations could simply be isolated examples or potentially anecdotal.

Economists typically measure the responsiveness of wages to immigrants using the wage elasticity of immigration—the percentage change in wages one can expect for a given percentage change in the quantity of immigrants. Literature on the U.S. labor market suggests the wage elasticity of immigration is about −0.2, meaning that if the number of migrants were to increase by 10 percent, then wages would fall by 2 percent, on average. However, this average masks substantial disagreements among economists who study immigration. Some economists have found that wages do not change at all with an increased supply of immigrants (Card 1990, Card and Peri 2016). Others, such as Harvard University economist George Borjas, find a greater wage elasticity of immigration that is between −0.3 and −0.4 (Borjas 2003, Borjas and Katz 2007).

One reason for the substantial disagreement about the effects of immigration on wages is that there are several different empirical methods that economists use to study the wage relationship even though there is a relatively uniform theory (Altonji and Card 1991). Each empirical method uses a different way of measuring variation in the quantity of immigrants to generate wage estimates. Dustmann, Schonberg, and Stuhler (2016) summarize the three major methods as (1) the national skill-cell approach, (2) the pure spatial approach, and (3) a mixed approach. The national skill-cell approach uses variation in the entry of immigrants to different education-experience groups within the national population. The pure spatial approach uses variation in the immigrant flow across cities or regions. The mixed approach uses variation in immigration inflows across both education groups and regions.

Different methodologies produce different elasticities. The skill-cell approach generates large estimates of the wage elasticity of immigration (Borjas 2003, Borjas and Katz 2007, Borjas 2014). Meanwhile, the pure spatial approach leads to estimates that vary substantially (Card 1990, 2009; Boustan, Fishback, and Kantor 2010). Finally, the mixed approach tends to lead to smaller, negative elasticity estimates that are not always significantly different from zero (Borjas 2006, Card and Lewis 2007, Lewis 2011). The method used to estimate the variation in the immigrant population is vital to producing the wage elasticity of immigration estimate. Dustmann, Schonberg and Stuhler (2016) argue that due to the difference in measuring variation between studies, estimates derived from the spatial approach and the skill-cell approach are fundamentally different models, even if derived from the same underlining theory.

Testing George Borjas’s Results

Immigration restrictionists use Borjas’s results, which rely on the national skill-cell method, to justify further diminishing legal immigration. If the wage elasticity of immigration is between −0.3 and −0.4, as Borjas argues, then a 10 percent increase in the number of immigrants within a specific education-experience cell is associated with a 3 to 4 percent decline in wages for workers within that cell. The effect, Borjas further argues, is even larger among workers who have less than a high school education. To the extent that poorly educated immigrants from Latin America compete with native workers, a reduction in the number of immigrants within specific education-experience cells would have a substantial, positive impact on the wages of American workers with the lowest educations.

At least two standard critiques of Borjas’s estimates are based on the assumptions in his model. The first critique is that his model’s skill-cell approach assumes that high school dropouts and those with a high school education are in different skill cells. Card (2009) and Ottaviano and Peri (2012) argue that high school dropouts and graduates are actually perfect substitutes—so migrants who enter skill cells among dropouts actually compete for jobs with a much larger proportion of the workforce. The second critique is that his model assumes that there is perfect substitutability between natives and immigrants within each skill cell. There are many reasons that immigrants and natives might not be perfect substitutes even if they have the same level of skill and education—for example, language ability (Lewis 2013). Card and Peri (2016) find that relaxing Borjas’s assumption of perfect substitution shows that an increased supply of immigrant workers actually increases wages.

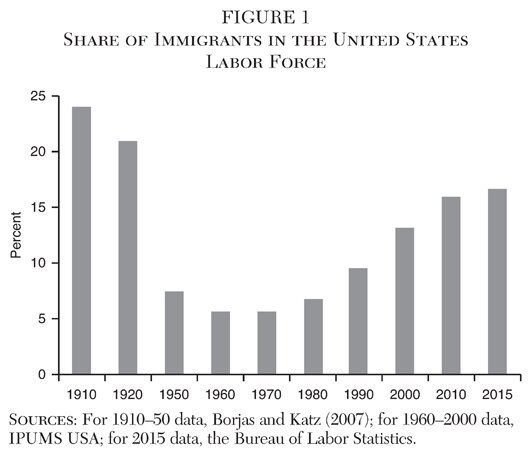
In a recent paper, my colleague Joe Russell and I set out to test the validity of Borjas’s result from a different perspective (de Brauw and Russell 2014). We use a replication method that recreates Borjas’s results and then tests them in two ways. First, we test whether Borjas’s estimates change when we add more years of data. Borjas’s initial study focused on the years 1960 to 2010. Specifically, we add the 2010 IPUMS data from the U.S. Census and estimate the wage elasticity using data from 1960 to 2010. The period between 1960 and 2000, studied by Borjas, was somewhat special: the share of foreign-born laborers in the United States was at an all-time low of 5.7 percent 1960 (Figure 1). At a result of that historical anomaly, the period between 1960 and 2000 might just reflect additional wage responsiveness as the number of immigrants rapidly climbed. The increase in the immigrant share of the labor force slowed between 2000 and 2010, so additional data could help reconcile Borjas’s results with the rest of the academic literature.

First, when we add the 2010 data, Borjas’s elasticity declines from −0.33 to −0.22. This result is important because adding one more Census year brings Borjas’s findings squarely in line with the rest of the academic literature. If Borjas’s model was correct on its own, simply adding data from 2010 should not have affected the elasticity estimate in the way that it did.

Second, if Borjas’s methodology is proper then it should also work to explain the relationship between the even larger influx of women workers into the labor force and wages that occurred from 1960 to 2010. Acemoglu, Autor, and Lyle (2004) call the climbing female labor force participation in the United States “one of the most profound labor market transformations of the past century.” If the assumptions behind Borjas’s model are appropriate for immigrants, in this case, implying that within education-experience cells men and women are perfect substitutes and that the national labor market should be considered, then it should also be appropriate for estimating the effect on men’s wages of women entering the labor force since 1960. To address the fact that women are more likely than men to move in and out of the labor force, to give birth and to raise children, we adjust the average experience of women of specific ages based on a computation by Regan and Oaxaca (2009), who measured average differences between potential and actual work experience among women.

When we use Borjas’s model that estimated the impacts of female labor force entry on men’s wages, we find a statistically insignificant relationship when we use weekly wages as the wage measure, but a positive and statistically significant relationship when using annual wages. This result implies that as women enter specific education-experience cells men’s wages actually increased. These coefficients suggest that Borjas’s method cannot be just measuring labor demand. Thus, the perfect substitutability assumption in Borjas’s model is violated because it requires a negative coefficient. In fact, our estimates suggest that men and women must complement each other within some skill cells rather than be substitutes.

Economic Implications of Immigration Restriction

Restricting immigration will not have a substantial positive impact on native wages, at least in real terms. The question then is: What types of alternative impacts might occur if migration was further restricted? There are at least two further potential impacts of further restricted immigration. First, some occupations like tomato harvesters could be automated such as they were in the late 1960s after the end of the bracero guest worker visa program (Schmitz and Seckler 1970; Clemens, Lewis, and Postel 2017). Automation would have a significant knock-on effect, but it would not raise the wages of low-skilled native workers who are substitutable with low-skilled immigrant workers. Second, certain types of laborers might drop out of the labor market altogether. Using spatial variation, Cortes and Tessada (2011) show that low-skilled immigration increases the labor market participation of high-skilled women by allowing families more freedom to hire child care or pay for other domestic tasks. An immigration decline could induce high-skilled women to leave the workforce as the cost of labor for such tasks would potentially rise.

Moreover, new immigration restrictions would likely have negative impacts on the economies of source countries. Personal remittances are 2.3 percent of Mexico’s GDP, 10.3 percent in Guatemala, 16.6 percent in El Salvador, and 18 percent in Honduras. Poverty in those countries would increase substantially without those remittances and American exports to that region would also decline. Further restricted immigration is more likely to increase poverty in Latin America and diminish U.S. exports than increase native wages.

Conclusion

Our research produced two broad results. First, when Borjas’s methods are extended a few years, the wage elasticity of immigration is −0.2 rather than −0.3 to −0.4. Second, Borjas’s assumption of perfect worker substitutability within cells cannot be correct as the wages of men and women both increased as women entered the workforce from 1960 to 2010. Empirical methods that relax the two assumptions described above likely lead to estimates that more accurately describe the impacts of immigration on native wages and that are either very small or zero (Ottaviano and Peri 2012, Ortega and Verdugo 2014).

References

Acemoglu, D.; Autor, D.; and Lyle, D. (2004) “Women, War, and Wages: The Effect of Female Labor Supply on the Wage Structure at Midcentury.” Journal of Political Economy 112 (3): 497–551.

Altonji, J. G., and Card, D. (1991) “The Effects of Immigration on the Labor Market Outcomes of Less-Skilled Natives.” In J. M. Abowd and R. B. Freeman (eds.) Immigration, Trade, and Labor. Chicago: University of Chicago Press.

Borjas, G. (2003) “The Labor Demand Curve Is Downward Sloping: Reexamining the Impact of Immigration on the Labor Market.” Quarterly Journal of Economics 118 (4):1335–74.

__________ (2006) “Native Internal Migration and the Labor Market Impact of Immigration.” Journal of Human Resources 41 (2): 221–58.

__________(2014) Immigration Economics. Cambridge, Mass.: Harvard University Press.

Borjas, G., and Katz, L. (2007) “The Evolution of the Mexican-Born Workforce in the United States.” In G. Borjas (ed.) Mexican Immigration to the United States, Cambridge, Mass.: National Bureau of Economic Research.

Boustan, L. P.; Fishback, P. V.; and Kantor, S. (2010) “The Effect of Internal Migration on Local Labor Markets: American Cities during the Great Depression.” Journal of Labor Economics 28 (4): 719–46.

Card, D. (1990) “The Impact of the Mariel Boatlift on the Miami Labor Market.” Industrial and Labor Relations Review 43 (2): 245–57.

__________ (2009) “How Immigration Affects U.S. Cities.” In R. Inman (ed.) Urban Enigma: City Problems, City Prospects. Princeton, N. J.: Princeton University Press.

Card, D., and Lewis, E. (2007) “The Diffusion of Mexican Immigrants during the 1990s: Explanations and Impacts.” In G. Borjas (ed.) Mexican Immigration to the United States. Cambridge, Mass.: National Bureau of Economic Research.

Card, D., and Peri, G. (2016) “Immigration Economics by George J. Borjas: A Review Essay.” Journal of Economic Literature 54 (4): 1333–49.

Clemens, M. (2013) “International Harvest: A Case Study of How Foreign Workers Help American Farms Grow Crops—and the Economy.” A report by the Partnership for the New American Economy and the Center for Global Development.

Clemens, M. A.; Lewis, E. G.; and Postel, H. M. (2017) “Immigration Restrictions as Active Labor Market Policy: Evidence from the Mexican Bracero Exclusion.” NBER Working Paper No. 23123.

Cortes, P., and Tessada, J. (2011) “Low-Skilled Immigration and the Labor Supply of Highly Skilled Women.” American Economic Journal: Applied Economics. 3 (3): 88–123.

de Brauw, A., and Russell, J. (2014) “Revisiting the Labor Demand Curve: The Wage Effects of Immigration and Women’s Entry into the U.S. Labor Force, 1960–2010.” International Food Policy Research Institute Discussion Paper No. 1402.

Dustmann, C.; Schonberg, U; and Stuhler, J. (2016) “The Impact of Immigration: Why Do Studies Reach Such Different Results?” Journal of Economic Perspectives 30 (4): 31–56.

Lewis, E. (2011) “Immigration, Skill Mix, and Capital Skill Complementarity.” Quarterly Journal of Economics 126 (2): 1029–69.

__________ (2013) “Immigrant-Native Substitutability and the Role of Language.” In D. Card and S. Raphael (eds.) Immigration, Poverty, and Socio-Economic Inequality. New York: Russell Sage Foundation.

Ortega, J., and Verdugo, G. (2014) “The Impact of Immigration on the French Labor Market: Why So Different?” Labour Economics 29: 14–27.

Ottaviano, G., and Peri, G. (2012) “Rethinking the Effects of Immigration on Wages.” Journal of the European Economic Association 10 (1): 152–97.

Regan, T. L., and Oaxaca, R. L. (2009) “Work Experience as a Source of Specification Error in Earnings Models: Implications for Gender Wage Decompositions.” Journal of Population Economics 22 (2): 463–99.

Schmitz, A., and Seckler, D. (1970) “Mechanized Agriculture and Social Welfare: The Case of the Tomato Harvester.” American Journal of Agricultural Economics 52 (4): 569–77.